主页 > 经典汇 > 质量体系 > 正文

【Cpk】单工序由多个工艺参数组成，如何计算Cpk？[没有数学和编程能力的不建议阅读]

发布时间：2023-09-03来源：未知 编辑：admin

广告位置（首页一通--图文）

之前有读者咨询我，如果有一道工序，它是由多个参数共同组成的，那么应该如何计算Cpk？

假如说我们某个激光工序加工一种材料，该道工序的工艺同时加工了三个尺寸：a、b、c，对应的只有上公差分别为：1.5、4、1。每个参数收集到的数据如下：

图片

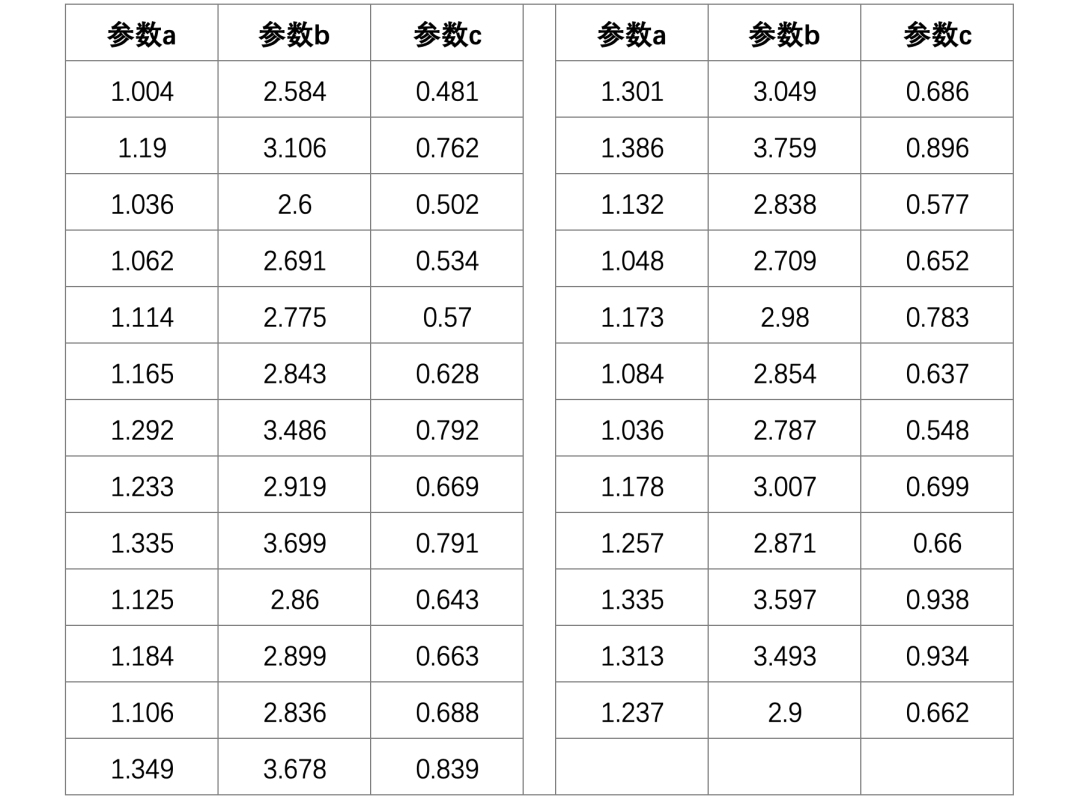
我们的做法有两种，第一种是按照我们传统的计算方法Cpk = min[(USL - μ) / 3σ, (μ - LSL) / 3σ]，将参数a、参数b、参数c分别计算出来，然后取三个参数中最小的那个Cpk作为参考。

根据上述方法我们计算得到：
Cpka = 0.928
Cpkb = 0.894
Cpkc = 0.819
0.819在上述三个值里面是最小值，我们可以用0.819来估计该工艺的Cpk。
 
另一种方法，我们可以用多元正态分布来计算，原理如下：
1. 计算成品率eta：对多元正态分布进行定积分，积分的上下限就是对应的公差上下限；
2. 计算σ水平，将eta代入超越方程 eta=Φ(1.5+p)-Φ(1.5-p)，其中p就是σ水平；

3. Cpk=p/3-0.5（这里减去0.5是考虑了偏移1.5σ，如果不考虑偏移可以不减0.5）。

Python编程代码如下：

  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
import pandas as pdfrom scipy.stats import mvnimport numpy as npimport mathfrom scipy.optimize import fsolve
#计算成品率etadf = pd.read_csv("/Users/admin/Desktop/sample.csv", encoding= 'utf-8') #读取数据源paramNames = df.columns.values #获取各列参数名myMatrix = [df[f'{param}'].tolist() for param in paramNames] #以参数列构建数列myMatrixCov = np.cov(myMatrix)  #计算协方差miu = np.mean(df.values, axis = 0)  #计算每列的均值low = np.array([0, 0, 0]) #参数的下限upp = np.array([1.5, 4, 1]) #参数的上限eta,i = mvn.mvnun(low,upp,miu,myMatrixCov)  #返回eta
#方程求解pσ中的p值def func(i):    x = i[0]    return [math.erf((1.5+x)/2**0.5)/2-math.erf((1.5-x)/2**0.5)/2-eta]p = fsolve(func,[0])
#多变量工序能力指数，这里的Cpk就是我们需要的值，当然这里包含了1.5σ偏倚Cpk = p/3-0.5

最终我们用程序跑出来的Cpk值如下：

图片

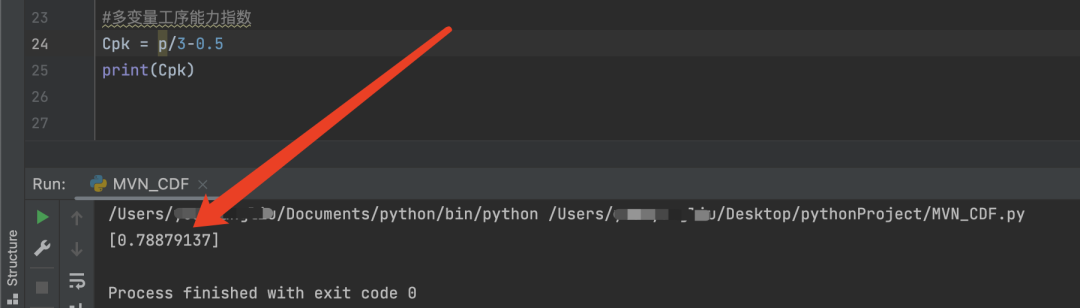
和第一种方法比较很明显，我们实际的Cpk = 0.789是要小于第一种方法得到的Cpk值（0.819），显而易见第一种方法高估了工艺水平。

大家都在评